COS (ROM-Routine)
Anmerkung: Dieser Artikel beschreibt die numerische COS-Routine im BASIC-ROM.
| Name: | COS | ||||||
| Beschreibung: | Cosinus des Fließkommaregisters FAC berechnen | ||||||
| Einsprungpunkt: | $E264 / 57956 | ||||||
| Übergebene Argumente: | |||||||
| Rückgabe-Werte: | |||||||
Die ROM-Routine COS[1] — manchmal auch als COSIN[2] bezeichnet — berechnet den Cosinus des im Fließkommaregister FAC gespeicherten Winkels. Ihr Einsprungpunkt ist in der Tabelle der BASIC-Funktionen an Adresse $A066 hinterlegt, so dass die Routine bei jeder Auswertung der Funktion COS vom BASIC-Interpreter aufgerufen wird. Der Winkel muss im Bogenmaß angegeben werden.
Nach dem Aufruf steht in FAC der Wert der trigonometrischen Funktion, während der Inhalt von ARG undefiniert ist. Neben dem Inhalt der Fließkommaregister FAC und ARG ändert COS auch das Hilfsregister an den Adressen 38/$26 bis 41/$29, das Fließkommaregister FAC#3 an den Adressen 87/$57 bis 91/$5B und das Tangens-Vorzeichenflag an Adresse 18/$12.
Algorithmus[Bearbeiten | Quelltext bearbeiten]
COS implementiert keine eigenständige Berechnung des Cosinus, sondern addiert nur π/2 zu dem im Fließkommaregister FAC gespeicherten Wert. Anschließend wird die im ROM unmittelbar nachfolgende Routine SIN ausgeführt, die die eigentliche Berechnung vornimmt. Die ROM-Routine COS nutzt also den Zusammenhang cos(x) = sin(x + π/2) aus.
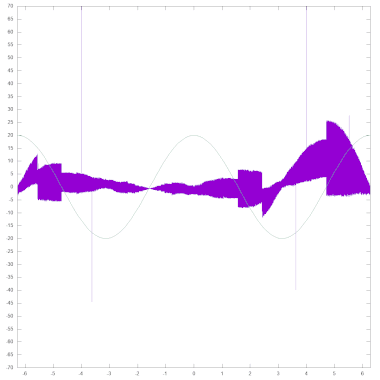
Das nachfolgende Schaubild zeigt die Abweichung zwischen dem von der COS-Routine gelieferten Wert und dem exakten Cosinus (violett, berechnet als Fließkommazahl mit doppelter Genauigkeit). Zur besseren Orientierung ist auch der Verlauf der Cosinus-Funktion eingezeichnet (grün, in y-Richtung gestreckt um den Faktor 20). Für die Erstellung des Schaubilds wurden die Werte nicht etwa mit PRINT ausgegeben, sondern es wurde der binäre Inhalt von FAC vor und nach dem Aufruf der COS-Routine ausgelesen. Auf diese Weise gehen keine Ungenauigkeiten oder eventuelle Fehler aus der Umwandlung von der Fließkommadarstellung nach ASCII in die Analyse ein. Zudem wurden als Argumente von COS nur die ganzzahligen Vielfachen von 2-15 im Intervall ]-π/2; π/2[ verwendet, um exakt äquidistante Eingabewerte betrachten zu können. Das Schaubild zeigt, dass die Abweichungen zwischen dem Ergebnis von COS und dem exakten Cosinus (von durchschnittlich 3.26E-10, maximal 25.75E-10, mit einzelnen Ausreißern von bis zu 190.93E-10 aufgrund eines Fehlers in der Multiplikationsroutine) durch den zusätzlichen Rechenschritt bei der Ableitung von SIN sich gegenüber den dortigen Werten noch deutlich erhöht haben, und dass dadurch zudem sprunghafte Änderungen bei ungeradzahligen Vielfachen von π/2 auftreten.
Laufzeitverhalten[Bearbeiten | Quelltext bearbeiten]
Der von COS mitverwendete Algorithmus sowie das Laufzeitverhalten sind ausführlich in der Beschreibung der ROM-Routine SIN dokumentiert. Zu den dort angegebenen Laufzeiten ist lediglich noch die Rechenzeit für das Addieren von π/2 zum FAC hinzuzurechnen.
Bugs[Bearbeiten | Quelltext bearbeiten]
- Wie aus dem obigen Schaubild mit den Abweichungen zwischen dem Ergebnis von COS und dem exakten Cosinus ersichtlich, zeigen sich die Auswirkungen eines Fehlers in FMULT auch in den Ergebnissen der hierauf aufbauenden ROM-Routine COS: Bei insgesamt 6 von 411775 Berechnungen der Analyse verursachte dieser Fehler eine Abweichung von mehr als 30E-10, im Extremfall — bei der Berechnung von COS(131449 / 32768) — sogar von 190.93E-10.
Weblinks[Bearbeiten | Quelltext bearbeiten]
- Disassembly von COS/$E264 auf All About Your 64

- CodeBase 64: Floating Point Math

- C64 BASIC & KERNAL ROM Disassembly von Michael Steil

- C64OS: Floating Point Math from BASIC
