SIN (ROM-Routine)

Anmerkung: Dieser Artikel beschreibt die numerische SIN-Routine im BASIC-ROM.

Name:			SIN
Beschreibung:			Sinus des Fließkommaregisters FAC berechnen
Einsprungpunkt:			$E26B / 57963
Übergebene Argumente:
Rückgabe-Werte:

Die ROM-Routine SIN — manchmal auch als SINUS bezeichnet — berechnet den Sinus des im Fließkommaregister FAC gespeicherten Winkels. Ihr Einsprungpunkt ist in der Tabelle der BASIC-Funktionen an Adresse $A068 hinterlegt, so dass die Routine bei jeder Auswertung der Funktion SIN vom BASIC-Interpreter aufgerufen wird. Der Winkel muss im Bogenmaß angegeben werden.

Nach dem Aufruf steht in FAC der Wert der trigonometrischen Funktion, während der Inhalt von ARG undefiniert ist. Neben dem Inhalt der Fließkommaregister FAC und ARG ändert SIN auch das Hilfsregister an den Adressen 38/$26 bis 41/$29, die Fließkommaregister FAC#3 und FAC#4 an den Adressen 87/$57 bis 96/$60 und das Tangens-Vorzeichenflag an Adresse 18/$12.

Algorithmus

Die Routine SIN führt nacheinander die folgenden Schritte aus:

1. FAC wird durch die Konstante 2π dividiert. Vom Resultat wird dann der ganzzahlige Anteil subtrahiert, so dass nur die Nachkommastellen verbleiben. Die Routine nutzt also die Periodizität der Sinusfunktion, um den in FAC übergebenen Winkel in das Intervall [0; 2π[ zu transferieren, und bildet dieses dann auf das Intervall [0; 1[ ab.
2. Liegt der so erhaltene Wert von FAC zwischen 0 und 0.25 (entsprechend einem ursprünglichen Winkel zwischen 0 und π/2), so kann er direkt weiterverarbeitet werden.
   Liegt FAC dagegen zwischen 0.25 und 0.75 (entsprechend einem ursprünglichen Winkel zwischen π/2 und 3π/2), so wird er durch den Wert 0.5 - FAC (entsprechend π - Winkel) ersetzt. Dieser Schritt nutzt die Symmetrie der Sinusfunktion zur Geraden mit der Gleichung x = π/2 aus, um FAC in den Bereich zwischen -0.25 und 0.25 (entsprechend einem Winkel zwischen -π/2 und π/2) zu bringen.
   Liegt der im ersten Schritt erhaltene Wert von FAC schließlich zwischen 0.75 und 1 (entsprechend einem ursprünglichen Winkel zwischen 3π/2 und 2π), so wird er durch FAC - 1 (entsprechend Winkel - 2π) ersetzt. Dieser Schritt nutzt die Periodizität der Sinusfunktion aus, um FAC in den Bereich zwischen -0.25 und 0 (entsprechend einem Winkel zwischen -π/2 und 0) zu bringen.
   In allen Fällen liegt FAC nun zwischen -0.25 und 0.25.
3. Der so transformierten Winkel wird nun in das folgende Polynom 11. Grades eingesetzt, das im Intervall [-0.5; 0.5[ die Funktion f(x) = sin(2π x) approximiert. Die zugehörigen Koeffizienten finden sich im ROM an Adresse $E2EF / 58095; der letzte Koeffizient in dieser Funktionsgleichung hat den Wert 2π. Zur Berechnung des Funktionswerts wird die ROM-Routine POLYX aufgerufen. Da der Wert von FAC im ersten Schritt durch 2π dividiert wurde, liefert dieses Polynom direkt einen Näherungswert für den Sinus des ursprünglichen Winkels:

p(x) = -14.38139067 x11 + 42.00779712 x9 - 76.70417026 x7 + 81.60522369 x5 - 41.34170210 x3 + 6.28318531 x

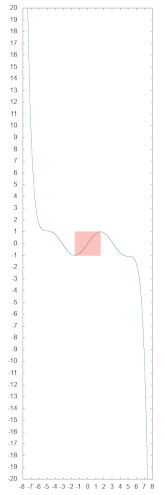
Die folgenden beiden Schaubilder zeigen den Graphen dieses Polynoms (grün). Aus Gründen der Anschaulichkeit ist dieser in x-Richtung um den Faktor 2π gestreckt, stellt also die Funktion q(x) = p(x / 2π) dar. In beiden Bildern ist das Intervall, das von der SIN-Routine genutzt wird, hellrot eingefärbt. Im rechten Bild ist zudem der Verlauf der Sinus-Funktion (violett) zum Vergleich eingezeichnet.

Die nächsten beiden Bilder veranschaulichen noch die Qualität der Approximation. Das linke Bild zeigt im Intervall [-π/2, π/2] die Abweichung zwischen dem Approximationspolynom und dem exakten Sinus (grün), multipliziert mit 10¹⁰. Diese Werte wurden als doppelt genaue Fließkommazahlen (52 Bit-Mantisse) berechnet. Der maximale Betrag der so ermittelten Abweichung zwischen q(x) und sin(x) liegt im betrachteten Intervall bei 1.58E-10. Zum Vergleich ist die Sinus-Funktion (violett) in das Schaubild eingezeichnet.

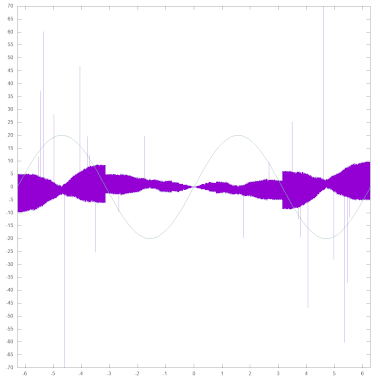
Das rechte Bild zeigt die Abweichung zwischen dem von der SIN-Routine gelieferten Wert und dem exakten Sinus (violett, wieder berechnet als Fließkommazahl mit doppelter Genauigkeit). Zur besseren Orientierung ist auch der Verlauf der Sinus-Funktion eingezeichnet (grün, in y-Richtung gestreckt um den Faktor 20). Für die Erstellung des Schaubilds wurden die Werte nicht etwa mit PRINT ausgegeben, sondern es wurde der binäre Inhalt von FAC vor und nach dem Aufruf der SIN-Routine ausgelesen. Auf diese Weise gehen keine Ungenauigkeiten oder eventuelle Fehler aus der Umwandlung von der Fließkommadarstellung nach ASCII in die Analyse ein. Zudem wurden als Argumente von SIN nur die ganzzahligen Vielfachen von 2^-15 im Intervall ]-π/2; π/2[ verwendet, um exakt äquidistante Eingabewerte betrachten zu können. Das Schaubild zeigt, dass die Abweichung zwischen Approximationspolynom und exaktem Sinus (von durchschnittlich 0.32E-10, maximal 1.58E-10) vernachlässigbar ist gegenüber den durch Rundungsfehler verursachten Differenzen (von durchschnittlich 1.88E-10, maximal 9.84E-10, mit einzelnen Ausreißern von bis zu 167.68E-10 aufgrund eines Fehlers in der Multiplikationsroutine).

Laufzeitverhalten

SIN wertet in jedem Fall das in Schritt 3 des Algorithmus angegebene Polynom aus. Da die in POLYX genutzten ROM-Routinen FADD und FMULT allerdings auf einen Summanden bzw. einen Faktor von 0 prüfen und in diesem Fall keine Addition bzw. Multiplikation durchführen, benötigt der Aufruf von SIN(0) nur 3544 Systemtakte. In allen anderen Fällen ist aufgrund der großen Zahl von Rechenoperationen ein funktionaler Zusammenhang zwischen dem in FAC übergebenen Winkel und der Laufzeit von SIN nicht erkennbar. Im Rahmen ausgiebiger Messreihen lag die Laufzeit von SIN zwischen 21340 und 27064 Systemtakten.
Ein Systemtakt entspricht auf dem Commodore 64 rund einer Mikrosekunde (μs). Im ungünstigsten Fall benötigt die SIN-Routine also etwas mehr als 27 Millisekunden (ms).

Bugs

• Wie aus dem obigen Schaubild mit den Abweichungen zwischen dem Ergebnis von SIN und dem exakten Sinus ersichtlich, zeigen sich die Auswirkungen eines Fehlers in FMULT auch in den Ergebnissen der hierauf aufbauenden ROM-Routine SIN: Bei insgesamt 20 von 1235319 Berechnungen der Analyse verursachte dieser Fehler eine Abweichung von mehr als 10E-10, im Extremfall — bei der Berechnung von SIN(151147 / 32768) — sogar von 167.68E-10.
• Im zweiten Schritt des Algorithmus wird der Wert von FAC durch mehrere Additionen in einen Wertebereich transferiert, der einem Winkel zwischen -π/2 und π/2 entspricht. Die hierbei auftretenden Rundungsfehler fallen insbesondere bei betragsmäßig kleinen Winkeln auf. So liefert SIN immer den Wert 0, sofern der Betrag des Winkels in FAC kleiner als 7.314590391E-10 ist. Diese Ungenauigkeit hätte sich dadurch vermeiden lassen, dass als Ergebnis von SIN einfach der unveränderte Wert von FAC zurückgegeben wird, sofern dessen Exponent eine gegebene Grenze (zum Beispiel 114, entsprechend einem Winkel mit einem Betrag von weniger als 3E-5) unterschreitet.

?SIN(8E-10),SIN(7E-10) 7.97176063E-10 0

Weblinks

• Disassembly von SIN/$E26B auf All About Your 64
• CodeBase 64: Floating Point Math
• C64 BASIC & KERNAL ROM Disassembly von Michael Steil
• C64OS: Floating Point Math from BASIC