FADD

Anmerkung: Dieser Artikel beschreibt die numerische FADD-Routine im BASIC-ROM, die allen Additionen und Subtraktionen im BASIC V2 des Commodore 64 zugrundeliegt.

Name:			FADD
Beschreibung:			Fließkommazahl aus dem Speicher nach ARG holen und zu FAC addieren
Einsprungpunkt:			$B867 / 47207
Übergebene Argumente:
Akkumulator:			Adresse Summand A (Low-Byte)
Y-Register:			Adresse Summand A (High-Byte)
Sonstige:			FAC = Summand B
Rückgabe-Werte:
Sonstige:			FAC = Ergebnis der Addition A+B, ARG = Summand A

FADD — manchmal auch als MEMPLUS, ADDMEM, M-ADD oder einfach als Plus bezeichnet — holt eine Fließkommazahl aus dem Speicher des C64 in das Fließkommaregister ARG und addiert sie dann zu dem bereits im Fließkommaregister FAC befindlichen Wert. Die Speicheradresse dieser Fließkommazahl wird im Akkumulator (Low-Byte) und im Y-Register (High-Byte) übergeben. Die Zahl muss im kompakten 5 Byte-Format vorliegen, wie es zum Speichern von REAL-Variablen verwendet wird. Es können sowohl Werte im RAM als auch Konstanten im BASIC-ROM adressiert werden.

Nach dem Aufruf steht in FAC das Ergebnis der Addition, während ARG weiterhin die aus dem Speicher gelesene Zahl enthält. Diese kann dann für nachfolgend aufgerufene Numerik-Routinen weiter verwendet werden. Ist das Ergebnis der Addition zu groß für die Fließkommadarstellung des C64, so löst FADD einen ?OVERFLOW ERROR aus. In diesem Fall ist FAC anschließend undefiniert, während ARG noch den Summanden aus dem Speicher enthält.

Neben dem Inhalt der Fließkommaregister FAC und ARG ändert FADD auch das Rundungsbyte des Hilfspuffers FAC#3 an Adresse 86/$56. Die innerhalb von FADD aufgerufene CONUPK-Routine überschreibt zudem den Hilfszeiger an den Adressen 34/$22 (Low-Byte) und 35/$23 (High-Byte).

Algorithmus

Die Routine FADD führt nacheinander die folgenden Schritte aus:

1. Die Routine CONUPK wird aufgerufen, um die zu addierende Fließkommazahl aus dem Speicher in das Fließkommaregister ARG zu kopieren. CONUPK vergleicht zudem die Vorzeichen von FAC und ARG und speichert das Ergebnis im höchstwertigen Bit von Adresse 111/$6F (0: Vorzeichen sind gleich, 1: Vorzeichen sind verschieden). Zuletzt lädt CONUPK den Exponenten des Fließkommaregisters FAC in den Akkumulator und setzt dadurch das Zero-Flag genau dann, wenn FAC gleich 0 ist. Diese beiden Schritte sind Voraussetzungen für die nachfolgende Addition.
2. Falls das Zero-Flag gesetzt ist, FAC also gleich 0 ist, so ist das Ergebnis der Addition von FAC und ARG gleich dem Wert von ARG. In diesem Fall wird nur der Inhalt des Fließkommaregisters ARG nach FAC umkopiert.
3. Ist das Zero-Flag dagegen gelöscht und somit FAC ungleich 0, so prüft die Routine als nächstes, ob ARG gleich 0 ist. Auch in diesem Fall ist keine weitere Berechnung erforderlich, da sich der Wert von FAC durch die Addition nicht ändert.
4. In allen anderen Fällen ist eine Addition erforderlich. Hierzu werden zunächst die Exponenten von FAC und ARG verglichen. Sind diese gleich, so kann sofort zur Addition übergegangen werden.
5. Ansonsten wird die Mantisse des Summanden mit dem kleineren Exponenten um so viele Bits nach rechts verschoben, wie die Differenz der Exponenten angibt. Wenn sich die Exponenten um 32 oder mehr unterscheiden (also mindestens um die Länge der Mantisse), so ist dieser Schritt eigentlich überflüssig, da sich dann durch die Addition der Wert des betragsmäßig größeren Summanden nicht ändert — aber diese Optimierungsmöglichkeit wird von FADD nicht genutzt. Die Rechtsverschiebung wird in zwei Phasen durchgeführt: Falls möglich zunächst byteweise (in Schritten von jeweils 8 Bit), anschließend bitweise.
6. Falls die beiden Summanden das gleiche Vorzeichen haben, so werden die Mantissen nun byteweise addiert. Ergibt sich hierbei ein Übertrag, so wird die Mantisse des Resultats um eine Stelle nach rechts verschoben und der Exponent um 1 erhöht. Sofern dies nicht möglich ist, weil der Exponent bereits den maximalen Wert $FF hatte, so resultiert hieraus ein ?OVERFLOW ERROR.
7. Haben die beiden Summanden dagegen verschiedene Vorzeichen, so wird die Mantisse des Summanden mit dem kleineren Betrag byteweise von der anderen Mantisse subtrahiert. Anschließend wird die Mantisse des Resultats normalisiert (durch Linksverschieben linksbündig gemacht) — wieder wenn möglich zunächst byteweise (in Schritten von 8 Bit) und anschließend bitweise. Die Zahl der Bits, um die die Mantisse des Resultats nach links verschoben wurde, wird anschließend vom Exponenten des Ergebnisses subtrahiert; falls dieser dadurch 0 wird oder gar ein Unterlauf entsteht, so ist das Ergebnis der Subtraktion kleiner als die kleinste darstellbare Zahl und wird daher auf 0 gesetzt. Ebenso wird das Ergebnis auf 0 gesetzt, wenn die Subtraktion das Ergebnis 0 hatte — dieser Sonderfall wird während des byteweisen Linksverschiebens dadurch erkannt, dass auch nach vier Schritten das höchstwertige Byte der Mantisse immer noch 0 ist.
8. Falls kein Überlauf aufgetreten ist, so steht im Fließkommaregister FAC nun das Ergebnis der Addition, während ARG immer noch den aus dem Speicher gelesenen Summanden enthält.

Laufzeitverhalten

• In jedem Fall wird zunächst von der Routine CONUPK die zu addierende Zahl aus dem Speicher geholt (typischerweise 85, in Sonderfällen bis zu 89 Systemtakte).
• Falls FAC gleich 0 ist, so wird nur ARG nach FAC umkopiert (plus 92 Takte).
• Falls ARG gleich 0 ist, so bleibt stattdessen FAC einfach unverändert (plus 31 Takte). Dank dieser Reihenfolge ist interessanterweise die Addition "0 + 0" langsamer als die Addition "1 + 0".
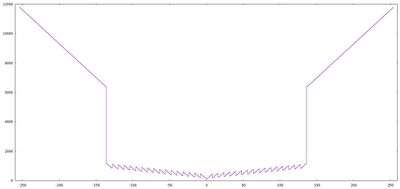
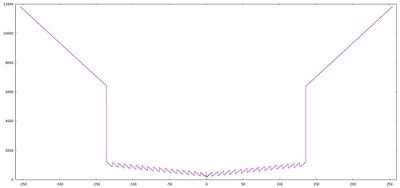
• Sind sowohl FAC als auch ARG ungleich 0, so illustrieren die nachfolgenden Schaubilder die zusätzliche Rechenzeit für die Addition. Das linke Bild zeigt den Fall zweier Summanden mit gleichem Vorzeichen (Addition der Beträge), das rechte Bild den Fall verschiedener Vorzeichen (Subtraktion der Beträge). Auf der Abszissenachse ist hierzu jeweils das Größenverhältnis der Summanden aufgetragen, gemessen als binärer Logarithmus lb(abs(ARG / FAC)), auf der Ordinatenachse die Dauer der Addition in Systemtakten.
  Deutlich erkennbar ist, dass die Laufzeit von FADD hauptsächlich durch das Rechtsverschieben des betragsmäßig kleineren Summanden vor der Addition bestimmt wird. Wichtigster Unterschied zwischen den beiden Schaubildern ist der zusätzliche Aufwand für die Normalisierung des Resultats bei der Subtraktion, falls sich die Beträge der Zahlen in FAC und ARG nur geringfügig unterscheiden.

Rechenzeitaufwand in Systemtakten bei der Addition, in Abhängigkeit der Differenz der Exponenten.

Rechenzeitaufwand in Systemtakten bei der Subtraktion, in Abhängigkeit der Differenz der Exponenten. In der Mitte der Abszissenachse ist der Zusatzaufwand für das Normalisieren des Resultats erkennbar.

• Bei der Addition ergibt sich die kürzeste Laufzeit bei der Addition zweier Summanden mit gleichem Exponenten, beispielsweise "1 + 1" (85 Systemtakte für CONUPK plus 123 Takte für die Addition). Am längsten dauert die Addition zweier betragsmäßig sehr unterschiedlicher Summanden, beispielsweise "3.0E-39 + 1.7E+38" (plus 11807 Takte für die Addition). Geringfügig schneller wird diese Berechnung, wenn der betragsmäßig größere der beiden Summanden im Fließkommaregister FAC steht, also "1.7E+38 + 3.0E-39" (plus 11790 Takte). Das Vorzeichen (beide Summanden positiv oder beide Summanden negativ) hat dagegen keinen Einfluss auf die Rechenzeit.
• Bei der Subtraktion ergibt sich die kürzeste Laufzeit, wenn Minuend und Subtrahend den gleichen Exponenten haben und der Exponent des Resultats um 1 geringer ist, beispielsweise "3 + (-2)" (85 Systemtakte für CONUPK plus 169 Takte für die Subtraktion). Am längsten dauert die Subtraktion zweier betragsmäßig sehr unterschiedlicher Werte, beispielsweise "3.0E-39 + (-1.7E+38)" (plus 11855 Takte für die Subtraktion). Geringfügig schneller wird diese Berechnung, wenn der betragsmäßig größere der beiden Werte im Fließkommaregister FAC steht, also "(-1.7E+38) + 3.0E-39" (plus 11837 Takte). Das Vorzeichen (betragsmäßig größerer Wert positiv oder negativ) hat auch hier keinen Einfluss auf die Rechenzeit.

Ein Systemtakt entspricht auf dem Commodore 64 rund einer Mikrosekunde (μs). Im ungünstigsten Fall benötigt die FADD-Routine also sowohl für eine Addition als auch für eine Subtraktion rund 12 Millisekunden (ms).

Bugs

Der Test, ob die Exponenten der beiden Summanden sich um mindestens 8 unterscheiden und somit der kleinere Summand zunächst byteweise nach rechts verschoben werden sollte, untersucht die negative Differenz der Exponenten:

B897: CMP #$F9  ; Negative Differenz der Exponenten in A mit der Konstanten -7 vergleichen
B899: BMI $B862 ; Zum byteweisen Verschieben verzweigen, falls Vergleichsergebnis negativ

Unterscheiden sich die Exponenten der beiden Summanden nun um 136 oder mehr, so beträgt die negative Differenz 120 oder weniger — und der Vergleichsbefehl setzt nicht das Negative-Flag, so dass fälschlicherweise nicht zunächst byteweise, sondern ausschließlich bitweise nach rechts verschoben wird. Korrekterweise sollte also nach diesem Vergleich stattdessen bei gelöschtem Carry-Flag verzweigt werden. Noch besser wäre natürlich ein zusätzlicher Test, ob sich die Exponenten um mindestens 32 (also mindestens um die Breite der Mantisse) unterscheiden — in diesem Fall kann der Summand mit dem kleineren Exponenten in analoger Weise ignoriert werden, wie dies im zweiten und dritten Schritt des Algorithmus bei Summanden mit einem Wert von 0 geschehen ist.

Das Ergebnis der Addition wird von dieser fehlerhaften Verzweigung nicht beeinflusst und bleibt korrekt (eine solche Addition ergibt ohnehin als Ergebnis einfach den betragsmäßig größeren Summanden), aber der Rechenzeitbedarf der FADD-Routine steigt stark an, wie aus den obigen Schaubildern ersichtlich ist.

Weblinks

• Disassembly von FADD/$B867 auf All About Your 64
• CodeBase 64: Floating Point Math
• C64 BASIC & KERNAL ROM Disassembly von Michael Steil
• C64OS: Floating Point Math from BASIC