EXP (ROM-Routine)

Aus C64-Wiki
Zur Navigation springenZur Suche springen

Anmerkung: Dieser Artikel beschreibt die numerische EXP-Routine im BASIC-ROM.

Name: EXP
Beschreibung: Natürliche Exponentialfunktion von Fließkommaregister FAC berechnen
Einsprungpunkt: $BFED / 49133
Übergebene Argumente:
Rückgabe-Werte:


Die ROM-Routine EXP[1][2] — manchmal auch als EHOCHF[3] bezeichnet — berechnet die natürliche Exponentialfunktion der im Fließkommaregister FAC gespeicherten Zahl. Ihr Einsprungpunkt ist in der Tabelle der BASIC-Funktionen an Adresse $A064 hinterlegt, so dass die Routine bei jeder Auswertung der Funktion EXP vom BASIC-Interpreter aufgerufen wird.

Nach dem Aufruf steht in FAC der Wert der Exponentialfunktion, während der Inhalt von ARG undefiniert ist. Ist das Ergebnis der Berechnung zu groß für die Fließkommadarstellung des C64, so löst EXP einen ?OVERFLOW ERROR aus. In diesem Fall ist der Inhalt von FAC undefiniert, während ARG das gerundete Produkt aus dem ursprünglichen Wert von FAC und der Konstanten 1/log(2) enthält.

Neben dem Inhalt der Fließkommaregister FAC und ARG ändert EXP auch den Mantissen-Puffer an Adresse 7/$07, den Zähler an Adresse 103/$67, die Hilfszeiger an den Adressen 34/$22 (Low-Byte) und 35/$23 (High-Byte) sowie 113/$71 (Low-Byte) und 114/$72 (High-Byte) und das Fließkommaregister FAC#4 an den Adressen 92/$5C bis 96/$60.

Algorithmus

EXP führt die Berechnung der natürlichen Exponentialfunktion — der Exponentialfunktion mit der Eulerschen Zahl e = 2.718281828... als Basis — zurück auf die Exponentialfunktion mit der Basis 2. Diese ist mit den vom C64 verwendeten Fließkommazahlen besonders einfach zu berechnen. EXP nutzt hierbei die folgende Umformung: 

exp(FAC) = 21/log(2) × FAC
  1. Als erstes multipliziert EXP die Zahl in FAC mit der Konstanten 1/log(2). Hierfür wird FMULT mit einem Zeiger auf Adresse $BFBF aufgerufen, wo diese Konstante im BASIC-ROM zu finden ist. Potenziert man anschließend die Zahl 2 mit dem so berechneten Produkt in FAC, so erhält man den gesuchten Wert der natürlichen Exponentialfunktion.
  2. Vor der eigentlichen Berechnung prüft EXP noch, ob das Ergebnis überhaupt auf dem C64 als Fließkommazahl dargestellt werden kann. Dies ist nur dann der Fall, wenn das Produkt in FAC betragsmäßig kleiner als 128 ist — erkennbar an einem Exponenten, der (einschließlich Exzess) kleiner als 136/$88 sein muss. Andernfalls löst EXP einen ?OVERFLOW ERROR aus, falls FAC größer oder gleich +128 ist, oder setzt das Ergebnis von EXP auf 0, falls FAC kleiner oder gleich -128 ist.
  3. Hat die erste Bereichsprüfung keinen Überlauf ergeben, so trennt EXP die Zahl in FAC nun in den ganzzahligen Anteil und die Nachkommastellen. Ist der ganzzahlige Anteil gleich 127, so wird das Ergebnis von EXP nicht im Fließkommaformat des C64 darstellbar sein, daher wird die Berechnung abgebrochen und stattdessen ein ?OVERFLOW ERROR gemeldet. Ansonsten kann der Faktor 2ganzzahliger Anteil später dadurch in den Wert von FAC einfließen, dass einfach der ganzzahlige Anteil zum Exponenten von FAC hinzuaddiert wird.
  4. Die aus den Nachkommastellen gebildete Zahl wird in das folgende Polynom[4] 7. Grades eingesetzt, das im Intervall [0; 1[ den Wert von 2Nachkommastellen approximiert:
    p(x) = 0.00002149876370 x7 + 0.0001435231404 x6 + 0.001342263482 x5 + 0.009614017014 x4 + 0.05550512686 x3 + 0.2402263846 x2 + 0.6931471862 x + 1
    Die Auswertung dieses Polynoms geschieht mit der ROM-Routine POLY, der beim Aufruf ein Zeiger auf die Koeffizienten an Adresse $BFC4 übergeben wird.
  5. Zuletzt wird noch der im dritten Schritt ermittelte ganzzahlige Anteil zum Exponenten von FAC addiert. Dies entspricht einer Multiplikation des Polynomwerts mit 2ganzzahliger Anteil. Das Resultat ist der gesuchte Wert der natürlichen Exponentialfunktion.

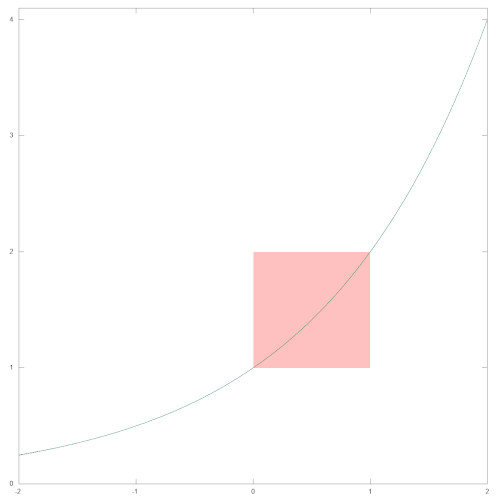
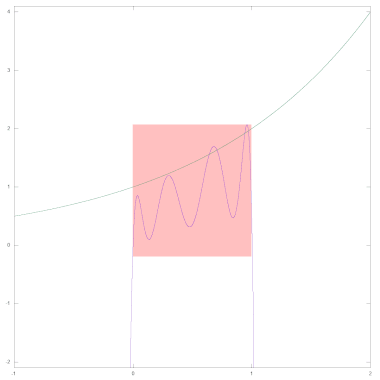
Die folgenden beiden Schaubilder zeigen den Graphen der Approximationspolynoms (violett). In beiden Bildern ist das Intervall, das von der EXP-Routine zur Approximation von 2x genutzt wird, hellrot eingefärbt. Zudem ist jeweils der Verlauf der Funktion 2x (grün) zum Vergleich eingezeichnet. Insbesondere das rechte Bild verdeutlicht, dass das Approximationspolynom auch außerhalb des von EXP genutzten Intervalls [0; 1[ eine sehr gute Näherung für 2x liefert.

exp large.gif
exp small.gif


Die nächsten beiden Bilder veranschaulichen noch die Qualität der Approximation. Das linke Bild zeigt im Intervall ]-1, 2] die Abweichung zwischen dem Approximationspolynom und dem Wert von 2x (violett), multipliziert mit 1010. Diese Werte wurden als doppelt genaue Fließkommazahlen (52 Bit-Mantisse) berechnet. Der maximale Betrag der so ermittelten Abweichung zwischen p(x) und 2x liegt im von EXP genutzten Intervall [0; 1[ bei 2.07E-10. Zum Vergleich ist die Funktion 2x in das Schaubild eingezeichnet (grün).

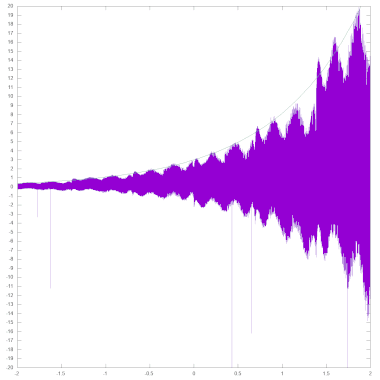
Das rechte Bild zeigt die Abweichung zwischen dem von der EXP-Routine gelieferten Wert und dem exakten Wert der natürlichen Exponentialfunktion (violett, wieder berechnet als Fließkommazahl mit doppelter Genauigkeit). Zur besseren Orientierung ist auch der Verlauf der Exponentialfunktion eingezeichnet (grün, in y-Richtung gestreckt um den Faktor 3). Für die Erstellung des Schaubilds wurden die Werte nicht etwa mit PRINT ausgegeben, sondern es wurde der binäre Inhalt von FAC vor und nach dem Aufruf der EXP-Routine ausgelesen. Auf diese Weise gehen keine Ungenauigkeiten oder eventuelle Fehler aus der Umwandlung von der Fließkommadarstellung nach ASCII in die Analyse ein. Zudem wurden als Argumente von EXP nur die ganzzahligen Vielfachen von 2-15 im Intervall ]-2; 2] verwendet, um exakt äquidistante Eingabewerte betrachten zu können. Das Schaubild zeigt, dass im Intervall [0; 1[ die Abweichung zwischen Approximationspolynom und exaktem Wert von 2x (von durchschnittlich 0.82E-10, maximal 2.03E-10) deutlich kleiner ist als die durch Rundungsfehler mitverursachten Differenzen zwischen EXP und der natürlichen Exponentialfunktion (von durchschnittlich 1.78E-10, maximal 7.80E-10, mit einzelnen Ausreißern von bis zu 179.55E-10 aufgrund eines Fehlers in der Multiplikationsroutine).

exp double error.gif
exp real error.gif


Laufzeitverhalten

Ist der Wert in FAC so klein, dass EXP den Wert 0 zurückliefert, so beträgt die beobachtete Laufzeit zwischen 1254 und 2391 Systemtakten.

Ansonsten führt EXP in jedem Fall alle Berechnungsschritte durch. Da die in POLY genutzten ROM-Routinen FADD und FMULT allerdings auf einen Summanden bzw. einen Faktor von 0 prüfen und in diesem Fall keine Addition bzw. Multiplikation durchführen, verkürzt sich die Laufzeit deutlich, sofern die in Schritt 3 des Algorithmus abgetrennten Nachkommastellen den Wert 0 haben. Dies ist immer dann der Fall, wenn beim Aufruf von EXP im Fließkommaregister FAC ein ganzzahliges Vielfaches von log(2) gespeichert ist. Für FAC = 0 benötigt EXP 3314 Systemtakte, für weitere Vielfache von log(2) zwischen 6035 Takten für 13 log(2) und 6625 Takten für -log(2).

In allen anderen Fällen ist aufgrund der großen Zahl von Rechenoperationen kein funktionaler Zusammenhang zwischen der in FAC übergebenen Zahl und der Laufzeit von EXP erkennbar. Die Rechenzeit lag im Rahmen ausgiebiger Messreihen zwischen 21796 und 26347 Systemtakten.

Ein Systemtakt entspricht auf dem Commodore 64 rund einer Mikrosekunde (μs). Im ungünstigsten Fall benötigt die EXP-Routine also etwa 26 Millisekunden (ms).

Bugs

  • Wie aus dem obigen Schaubild mit den Abweichungen zwischen dem Ergebnis von EXP und dem exakten Wert der natürlichen Exponentialfunktion ersichtlich, zeigen sich die Auswirkungen eines Fehlers in FMULT auch in den Ergebnissen der hierauf aufbauenden ROM-Routine EXP: Bei 5 von 131072 Berechnungen der Analyse trat dieser Fehler auf und verursachte im Extremfall — bei der Berechnung von EXP(14171 / 32768) — eine Abweichung von 179.55E-10.
  • Die Trennung von FAC in ganzzahligen Anteil und Nachkommastellen im dritten Schritt des Algorithmus geschieht, indem zunächst FAC nach ARG kopiert und dann die INT-Routine auf FAC angewendet wird. Die Ermittlung der Nachkommastellen als Differenz ARG - FAC könnte anschließend einfach durch Aufruf von FSUB geschehen — stattdessen vertauscht aber EXP byteweise den Inhalt von FAC und ARG, ruft erst dann FSUB auf und invertiert zuletzt das Vorzeichen des Resultats. Diese umständliche Vorgehensweise lässt eher auf eine Implementierung per "Versuch und Irrtum" als auf eine wohldurchdachte Berechnung schließen.

Weblinks

Quellen

  1. ↑ Florian Müller: C64 für Insider, S. 466
  2. ↑ Said Baloui/Rolf Brückmann/Lothar Englisch/Jacques Felt/Ralf Gelfand/Klaus Gerits/Darko Krsnik: Das neue Commodore 64 Intern Buch, S. 659
  3. ↑ Winfried Kassera/Frank Kassera: C64 Programmieren in Maschinensprache, S. 300
  4. ↑ John Fraser Hart et al.: Computer Approximations, John Wiley & Sons, Inc. 1968, S. 204 (Polynom 1044)
Abgerufen von „https://www.c64-wiki.de/index.php?title=EXP_(ROM-Routine)&oldid=236854“