QINT

Anmerkung: Dieser Artikel beschreibt die numerische QINT-Routine im BASIC-ROM.

Name:			QINT
Beschreibung:			Zahl im Fließkommaregister FAC in 32-Bit-Ganzzahl wandeln
Einsprungpunkt:			$BC9B / 48283
Übergebene Argumente:
Rückgabe-Werte:

QINT — manchmal auch als FACINT bezeichnet — wandelt den Inhalt des Fließkommaregisters FAC in eine 32-Bit-Ganzzahl um, wobei alle Nachkommastellen abgeschnitten und der Wert der Zahl falls nötig auf die nächstkleinere ganze Zahl abgerundet wird. Die Zahl wird im Big-Endian-Format gespeichert, so dass das höchstwertige Byte nach dem Aufruf im 1. Mantissenbyte an Adresse 98/$62, das niederwertigste Byte im 4. Mantissenbyte an Adresse 101/$65 steht. Negative Ganzzahlen werden in der Zweierkomplement-Darstellung gespeichert. Die in FAC übergebene Fließkommazahl muss im Intervall [ -2³¹-1; 2³¹-1 ] liegen.

Die ROM-Routine QINT verändert nur den Inhalt des Fließkommaregisters FAC. Sie ist die Grundlage für die Routinen FACINX und INT und wird im BASIC-ROM auch beim Setzen der Systemzeit TI$, beim Ausgeben von Fließkommazahlen als String und beim Verarbeiten von Speicheradressen, also bei den Befehlen PEEK, POKE, SYS und WAIT, aufgerufen.

Laufzeitverhalten

QINT prüft lediglich auf den Sonderfall FAC = 0 und liefert hierfür bereits nach 32 Systemtakten die Ganzzahl 0 zurück. Alle anderen Fließkommawerte werden ihrem Exponenten entsprechend so lange nach rechts verschoben, bis die Binärstelle mit der Wertigkeit 2⁰ im niederwertigsten Bit des 4. Mantissenbyte steht. Die geringsten Laufzeiten ergeben sich daher, wenn der Betrag von FAC im Intervall [2³⁰, 2³¹-1] liegt (93 Takte für positive, 186 Takte für negative Zahlen). Am längsten dauert die Umwandlung von betragsmäßig sehr kleinen Zahlen: Für FAC = 2^-128 liefert QINT nach 7361 Systemtakten das Resultat 0 ($00000000), für FAC = -2^-128 erst nach 8244 Takten das Ergebnis -1 ($FFFFFFFF).

Das nachfolgende Schaubild illustriert die Rechenzeit für die Umwandlung einer Fließkommazahl in eine Ganzzahl in Abhängigkeit des Exponenten (ohne Exzess). Der grüne Graph stellt die Laufzeit für negative, der violette die Laufzeit für positive Fließkommazahlen dar.

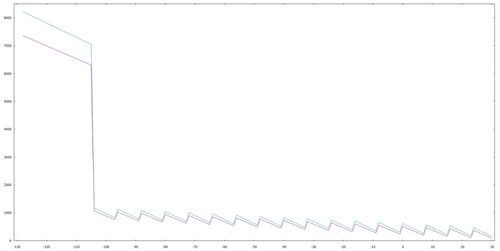
Ein Systemtakt entspricht auf dem Commodore 64 rund einer Mikrosekunde (μs). Im ungünstigsten Fall benötigt die QINT-Routine also für die Umwandlung rund 8 Millisekunden (ms).

Bugs

• Auch die Zahl -2³¹ lässt sich als 32-Bit-Ganzzahl im Zweierkomplement darstellen. Allerdings verschiebt QINT in diesem Fall die Mantisse von FAC 256 Mal um eine Stelle nach rechts und liefert schließlich nach einer Laufzeit von 13166 Systemtakten das inkorrekte Resultat -1 ($FFFFFFFF).
• Der Test, ob die Mantisse von FAC zunächst byteweise nach rechts verschoben werden sollte, subtrahiert 160 (also den Exzess plus die Länge der Mantisse) vom Exponenten und untersucht dann das Resultat:
  BCB1: CMP #$F9 ; Exponent-160 in A mit der Konstanten -7 vergleichen
BCB3: BPL $BCBB ; Zum bitweisen Verschieben verzweigen, falls Vergleichsergebnis positiv
  Ist der ursprüngliche Exponent nun einschließlich Exzess kleiner als 24, so hat A den Wert 120 oder weniger — und der Vergleichsbefehl setzt nicht das Negative-Flag, so dass fälschlicherweise nicht zunächst byteweise, sondern ausschließlich bitweise nach rechts verschoben wird und die Laufzeit stark ansteigt. Korrekterweise sollte also nach diesem Vergleich stattdessen bei gelöschtem Carry-Flag verzweigt werden. Noch besser wäre natürlich ein zusätzlicher Test, ob der ursprüngliche Exponent einschließlich Exzess kleiner als 129/$81 ist — in diesem Fall kann für positive Zahlen direkt der Wert 0, für negative Zahlen der Wert -1 zurückgegeben werden.

Weblinks

• Disassembly von QINT/$BC9B auf All About Your 64
• CodeBase 64: Floating Point Math
• C64 BASIC & KERNAL ROM Disassembly von Michael Steil
• C64OS: Floating Point Math from BASIC